Qual o melhor copo para beber cerveja, de acordo com a matemática?
Engenheiro da UFSJ calculou o formato ideal que um copo deve ter para manter o líquido dentro dele o mais gelado possível.

Os meses de calor no Brasil já batem na porta, e, honestamente, é insuportável – em alguns pontos do país as médias de temperatura aumentaram em até 3°C nos últimos 60 anos. Nessas épocas só dá para viver abraçado a um ventilador, fechado no ar condicionado ou adotar a rotina dos hipopótamos: passar boa parte do dia imerso na água.
Existem soluções mais brasileiras, como aceitar que o calor veio para ficar e tomar uma cerveja gelada. Problema mesmo é quando o copo americano (ou copo lagoinha, caso você more em Belo Horizonte) não consegue manter a cerveja trincando. Por mais comum que essa realidade seja, ela é frustrante.
O engenheiro mecânico Cláudio de Castro Pellegrini, da Universidade Federal de São João del-Rei, conta de um dia em que estava na borda da piscina, e se incomodou com a temperatura da sua cerveja.
“No cenário mais crítico, como na praia em um dia quente [38 ºC], apenas 3 minutos podem ser suficientes para tornar a cerveja intragável,” escreveu.
Em um estudo recente, ele investiga qual é o melhor copo para beber cerveja, de forma a deixá-la gelada pelo maior tempo possível. Para a Super, ele conta que uniu suas duas paixões no estudo: “eu diria que atingi minha meta estabelecida quando jovem: escrevi um artigo em que tanto o tema quanto o tom são divertidos. E o trem é didático, ainda por cima!”
A primeira versão do estudo saiu em 2019 na Revista Brasileira do Ensino de Física (RBEF), revista científica que Pellegrini assinava alguns textos. Ele conta que lançou duas versões, “uma com o tom relativamente formal e um ou outro pé de página engraçadinho”.
Em outubro desse ano ele publicou uma versão aprimorada, melhorando a metodologia e evitando os resultados irreais da primeira versão. O novo estudo elimina copos com aberturas mastodônticas e copos com 100 litros.
Sabendo disso, o pesquisador propõe a seguinte pergunta: “qual o formato do copo ideal para minimizar a troca de calor durante o consumo da bebida?”
Como criar o copo perfeito?
O primeiro desafio é evitar a absorção de calor ao máximo. O modelo mais simples seria usar um recipiente com a menor área superficial possível em relação ao volume – dessa forma, o calor externo penetra menos, mantendo a cerveja fria por mais tempo. Em três dimensões, a forma que tem a menor área superficial em relação ao seu volume é a esfera. Na teoria, esse seria o melhor formato. Mas um copo esférico, parecido com um aquário de peixe betta, não seria prático.
Vale ressaltar que o autor não estava interessado num cenário estático, em que a cerveja apenas esquenta no copo. Pensando na vida boêmia, Pellegrini escreve que “o processo aqui é bastante simples: pede-se uma cerveja, o garçom entrega, é servida, é consumida. Repete”. Esse foi o jeitinho que o pesquisador encontrou para explicar que a quantidade de líquido dentro do copo estaria em constante mudança. Nesse cenário, quanto mais vazio o copo, mais superfícies do vidro entram em contato com o ambiente externo.
Para a criação da equação, Pellegrini teve que ignorar algumas questões, como o calor que seria transferido da mão da pessoa segurando o vidro (ele só levou em conta o calor ambiente) e as ações de isolante térmico da espuma da cerveja.
Ele adicionou outros pré-requisitos: a base do copo teria que ser plana, isolante, e grande o suficiente para fazer o vidro ficar em pé. Além disso, o vidro deveria ser simétrico.
Com tudo isso em mente, o professor ainda colocou algumas condições para a fórmula: Pellegrini assumiu que a base do vidro seria um isolante térmico perfeito, mesmo que isso fosse impossível, que a densidade da bebida seria uniforme e que a temperatura da cerveja seria a mesma em todo o líquido.
A fórmula perfeita
Engana quem pensa que seria fácil assim. Reunindo o que já foi estabelecido, era preciso criar uma fórmula que definisse a mudança de temperatura da cerveja ao longo do tempo. Foi aí que o professor pensou no seguinte:
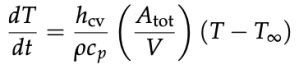
T é a temperatura da cerveja, ρ é a densidade, V é o volume, hCV é o coeficiente de transferência de calor por convecção, cp é a capacidade calorífica específica (o quão difícil é aquecer uma substância), T∞ é a temperatura ambiente, e Atot é a superfície exposta da cerveja (incluindo as laterais e a superfície circular superior).
Por mais que as letras acima pareçam uma equação de outro planeta, é simplesmente uma equação diferencial, conteúdo que se aprende no ensino médio. Trata-se de uma equação que envolve uma ou mais derivadas de uma função desconhecida, a incógnita. Ela descreve como uma quantidade varia em relação a outra. Neste caso, falamos sobre a mudança de temperatura na variável que é o copo.
Com essa fórmula (ou com alguns dias fritando no sol do Rio de Janeiro), dá para chegar em quatro conclusões: a primeira é que, quanto menor a temperatura ambiente, mais a cerveja demora a esquentar. Segundo: vale também deixar o copo longe de correntes de ar, que aumentam a transferência de calor por convecção.
O colarinho da cerveja é importante também: uma certa quantidade de espuma evita que a bebida perca dióxido de carbono muito rápido. Por fim, o uso de materiais mais espessos e isolantes, como a cerâmica, também diminuem o coeficiente de condução de calor. Porém, Pellegrini escreve que a mudança, “infelizmente, torna o contato labial desconfortável.”
O copo ideal
Pellegrini focou em minimizar o quociente Atot / V (superfície exposta da cerveja por volume), que representa o formato do copo. Ele derivou esse quociente, igualou a zero e, usando as propriedades dos corpos de revolução, obteve uma fórmula para o raio ideal (r) de um copo de cerveja perfeito em função da altura (h).

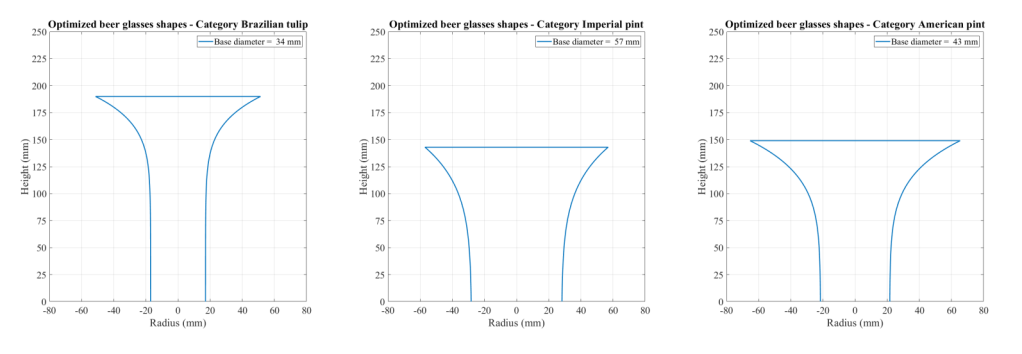
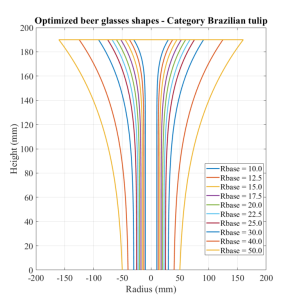
A fórmula sugere que o copo ideal deve ter uma abertura ampla e se estreitar em direção à base, semelhante a muitos copos de cerveja comuns. No entanto, copos reais frequentemente têm uma forma curva em S. A forma exata do copo ideal depende do raio da base e de uma constante C, que é influenciada pela altura do copo. Pellegrini calculou as formas ideais para copos com 19 cm de altura e diferentes raios de base. O formato resultante lembra uma taça de champanhe.
Com essa fórmula foi possível adaptar os copos já existentes para o tamanho perfeito, mudando o tamanho do raio das bases.
Qual é o defeito dos copos atuais?
“Eu não diria que são defeitos, mas os copos são concebidos com preocupações estéticas, desconsiderando a troca térmica”, explica o professor para a Super. O formato ideal lembra uma flor copo-de-leite, ou uma taça de champanhe.
Mesmo assim, os modelos já existentes tem seu valor: um copo americano, por exemplo, é pequeno o suficiente para que as pessoas bebam a cerveja antes que ela esquente completamente.
“Quer saber como seria um copo ‘ótimo dos ótimos dos ótimos’? Seria uma caneca de dupla parede evacuada, ou feita de cerâmica porosa que é mais barata, com formato dado pela minha fórmula, uma alça para isolar o calor da mão e uma tampa para reduzir a convecção pela abertura. Vai ser muito feio mas muito bom”, reflete Pellegrini.
Quando sai o copo perfeito?
Por hora, ainda não se sabe quando será possível colocar as mãos nesse exemplar. O professor lamenta por não ter os meios para que a construção aconteça. “Tenho ideia de usar uma impressora 3D mas confesso que não tenho maiores conhecimentos sobre o uso do equipamento.”
O que dá para saber é que o projeto ainda não acabou. O professor conta que pretende continuar a cruzada em busca do copo que ele chama de ‘ótimo dos ótimos dos ótimos’. Além disso, menciona que pretende incluir em projetos futuros fatores que foram descartados neste, como a troca térmica pelo fundo e a espuma da cerveja.
O único problema é que, para que esses efeitos sejam incluídos, a equação final que fornece a fórmula do formato do copo deve ter uma solução analítica. Ele diz que resultados atingidos por meio de simulações não o interessam.
“Nada contra simulação, a questão aqui é muito pessoal: sou de opinião que as soluções analíticas contém mais informação e são muito mais bonitas do que resultados de simulação.”



















