Matemático pode ter resolvido o “problema do sofá”
Já esteve de mudança e se perguntou se o sofá passa por aquele cantinho estreito? Os matemáticos têm a resposta.

Friends, quinta temporada, episódio 16. Ross compra um sofá novo e pede a ajuda de Rachel e Chandler para carregá-lo até o apartamento, usando as escadas. O móvel é grande demais e não consegue passar por um canto, ficando preso entre um andar e outro. Essa é uma das cenas clássicas e favoritas entre os fãs da série. Assista abaixo.
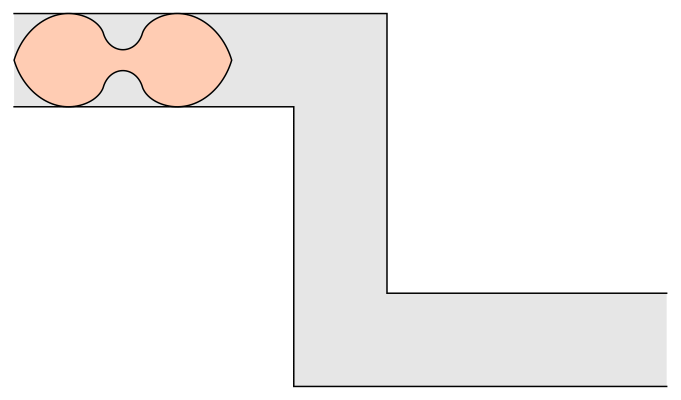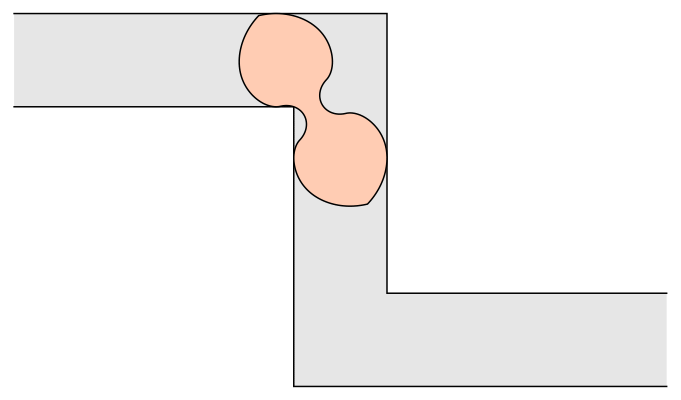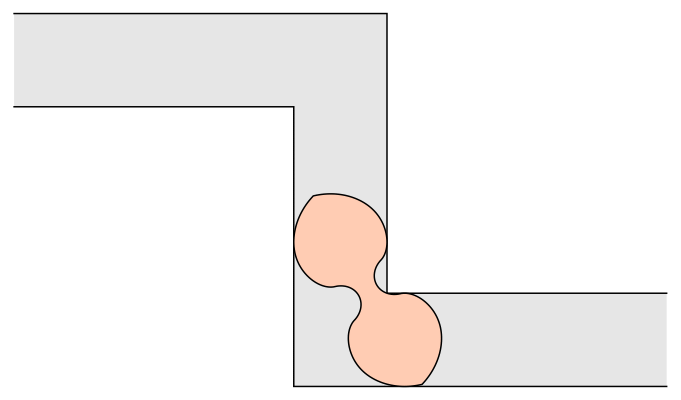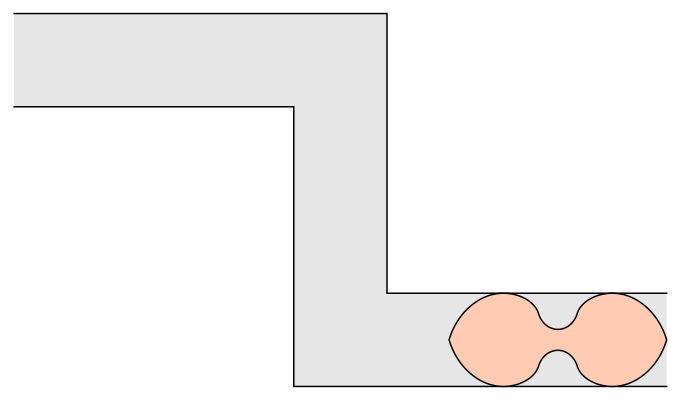
A cena é um bom exemplo do “problema do sofá” na matemática. Em 1966, o matemático Leo Moser propôs a seguinte questão: qual é o maior objeto bidimensional que consegue passar por um canto em formato de L? Desde então, alguns avanços foram feitos na área, mas sem encontrar uma resposta definitiva.
Considerando um corredor com um metro de largura, um móvel quadrado de 1m² passaria com tranquilidade. Mas um retângulo de dois metros de largura por um metro de comprimento já não conseguiria atravessar.
(No problema do sofá, os matemáticos não se referem a metros quadrados, e sim a unidades de área. O corredor pode ter um cm², m², km² ou ft², e o problema continua valendo. Um retângulo de 2m², por exemplo, tem duas unidades de área).

Mas e se o sofá não fosse quadrado ou retângulo, e sim um arco? Dois anos após o problema ser proposto, o matemático britânico John Hammersley descobriu um formato que conseguiria atravessar o canto, mesmo com mais de duas unidades de área. Ele provou que o sofá desse formato em específico pode ter até 2,2074 unidades de área e ainda passar pelo corredor. Veja abaixo.
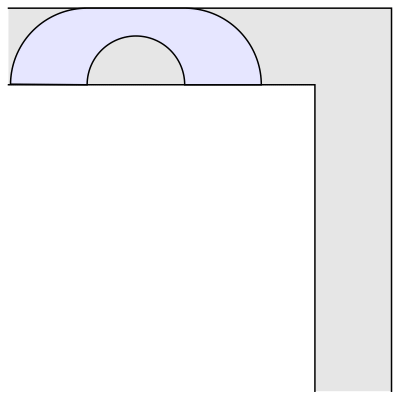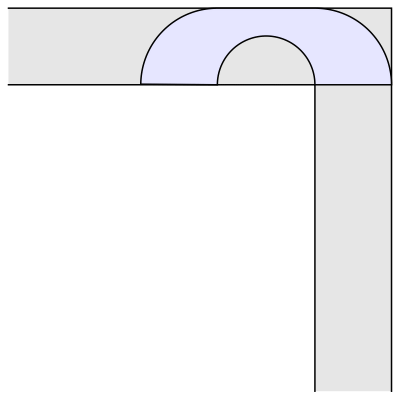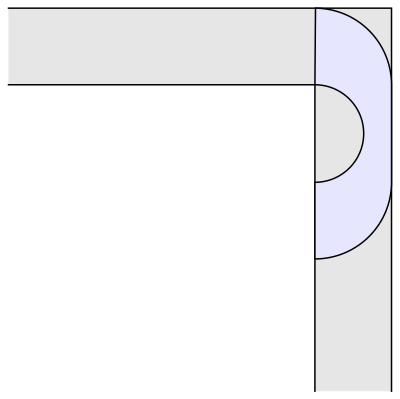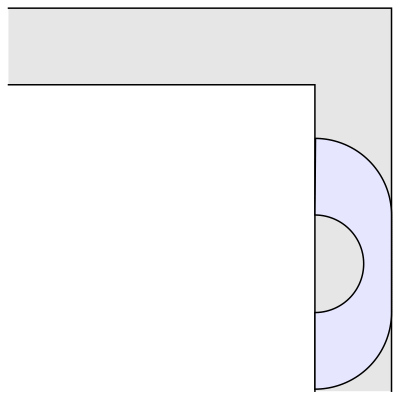
Em 1992, o matemático Joseph Gerver fez algumas mudanças no sofá de Hammersley, como deixar as pontas mais arredondadas. Com o novo formato, o sofá pode ter até 2,2195 unidades de área e atravessar o canto. Foi um avanço pequeno, mas significativo entre os matemáticos que tentam responder a pergunta proposta em 1966.

Agora, o matemático Jineon Baek da Universidade Yonsei, na Coreia do Sul, provou que 2,2195 unidades de área é o tamanho máximo que o sofá de Gerver pode ter. Baek usou uma ferramenta matemática chamada função injectiva e mais de 100 páginas do artigo para provar a tese. A pesquisa ainda não foi publicada em um periódico especializado, mas está disponível em um repositório de pré-prints.
Se o seu corredor tiver duas curvas em forma de L, boa sorte: você deve procurar por um sofá de Romik, que é provavelmente o maior formato capaz de passar pelos dois cantos.